Problem
A non-empty array A consisting of N integers is given. A pair of integers (P, Q), such that 0 ≤ P ≤ Q < N, is called a slice of array A. The sum of a slice (P, Q) is the total of A[P] + A[P+1] + ... + A[Q].
Write a function:
int solution(vector<int> &A);
that, given an array A consisting of N integers, returns the maximum sum of any slice of A.
For example, given array A such that:
A[0] = 3 A[1] = 2 A[2] = -6 A[3] = 4 A[4] = 0
the function should return 5 because:
- (3, 4) is a slice of A that has sum 4,
- (2, 2) is a slice of A that has sum −6,
- (0, 1) is a slice of A that has sum 5,
- no other slice of A has sum greater than (0, 1).
Write an efficient algorithm for the following assumptions:
- N is an integer within the range [1..1,000,000];
- each element of array A is an integer within the range [−1,000,000..1,000,000];
- the result will be an integer within the range [−2,147,483,648..2,147,483,647].
How to solve
- 정보
N의 길이를 가진 배열 A
- 구해야 하는것?
배열 A에서 연속되는 수의 합이 가장 큰 수 return
- 예시
A: 3 2 -6 4 0 인 경우, 3+2=5 가장 크므로 5 return
- 풀이
1)변수 초기화
cur_sum: 현재 최대 합
max_sum: 전체 최대 합
2) cur_sum 과 max_sum A[0] 로 초기화
3) A배열의 크기가 1이라면, A[0] return
4) 배열을 순회하며, cur_sum 과 max_sum 계산
- cur_sum = max(A[i], cur_sum+A[i]);
현재 합은 현재 A 배열의 값과, 이전까지의 합 cur_sum에 A 배열을 합한 값 중 큰 수 이다.
즉, 지금까지의 합에 A[i] 를 더한 값보다 A[i]가 더 크다면
cur_sum의 최대는 다시 A[i]로 초기화되는 것이다.
- max_sum = max(max_sum, cur_sum);
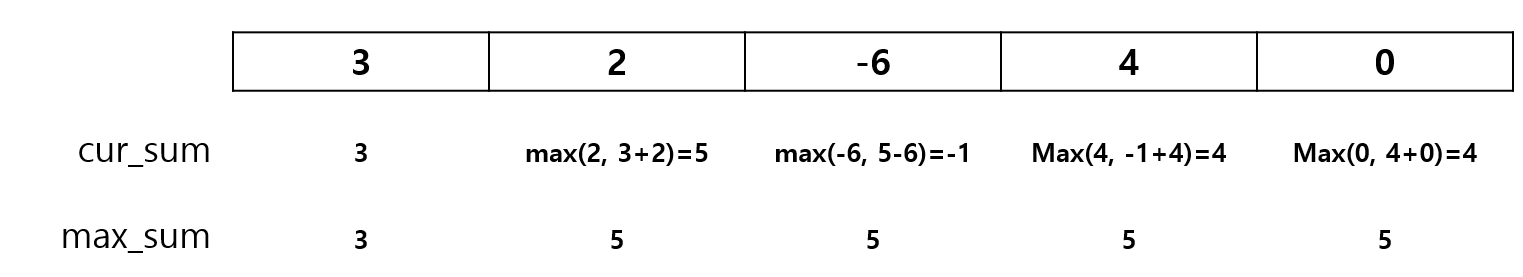
Solution(c++)
// you can use includes, for example:
#include <bits/stdc++.h>
// you can write to stdout for debugging purposes, e.g.
// cout << "this is a debug message" << endl;
int solution(vector<int> &A) {
int len = A.size();
int max_sum = A[0];
int cur_sum = A[0];
if(len == 1){
return A[0];
}
// write your code in C++14 (g++ 6.2.0)
for(int i=1; i<len; i++){
cur_sum = max(A[i], cur_sum+A[i]);
max_sum = max(max_sum, cur_sum);
}
return max_sum;
}
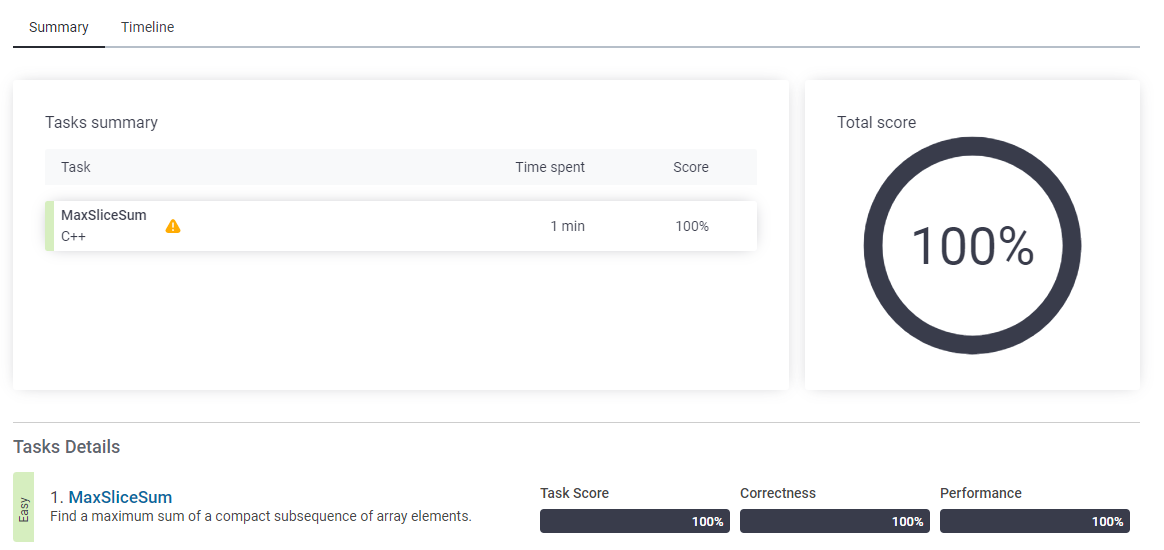
Test Result
app.codility.com/demo/results/trainingMPZ45S-FC9/
Test results - Codility
A non-empty array A consisting of N integers is given. A pair of integers (P, Q), such that 0 ≤ P ≤ Q < N, is called a slice of array A. The sum of a slice (P, Q) is the total of A[P] + A[P+1] + ... + A[Q]. Write a function: int solution(vector &A); th
app.codility.com

'SW > 알고리즘 문제풀이' 카테고리의 다른 글
| [Atcoder] D - Friends (C++) (1) | 2021.01.13 |
|---|---|
| [Codility] Lesson10 - Prime and Composite numbers : CountFactors (c++) (1) | 2021.01.12 |
| [Codility] Lesson9 - Maximum slice problem : MaxProfit (0) | 2021.01.08 |
| [Codility] Lesson8 - Leader : EquiLeader (c++) (0) | 2021.01.07 |
| [Codility] Lesson8 - Leader : Dominator (c++) (0) | 2021.01.04 |


댓글