[Codility] Lesson12 - Euclidean algorithm: Common Prime Divisors

Problem

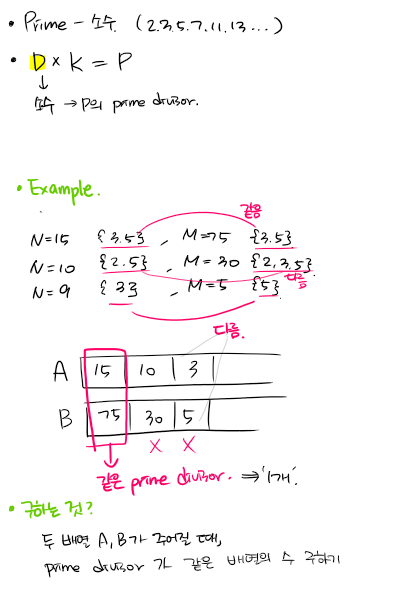
A prime is a positive integer X that has exactly two distinct divisors: 1 and X. The first few prime integers are 2, 3, 5, 7, 11 and 13.

A prime D is called a prime divisor of a positive integer P if there exists a positive integer K such that D * K = P. For example, 2 and 5 are prime divisors of 20.

You are given two positive integers N and M. The goal is to check whether the sets of prime divisors of integers N and M are exactly the same.

For example, given:

• N = 15 and M = 75, the prime divisors are the same: {3, 5};
• N = 10 and M = 30, the prime divisors aren't the same: {2, 5} is not equal to {2, 3, 5};
• N = 9 and M = 5, the prime divisors aren't the same: {3} is not equal to {5}.

Write a function:

class Solution { public int solution(int[] A, int[] B); }

that, given two non-empty arrays A and B of Z integers, returns the number of positions K for which the prime divisors of A[K] and B[K] are exactly the same.

For example, given:

A[0] = 15 B[0] = 75 A[1] = 10 B[1] = 30 A[2] = 3 B[2] = 5

the function should return 1, because only one pair (15, 75) has the same set of prime divisors.

Write an efficient algorithm for the following assumptions:

• Z is an integer within the range [1..6,000];
• each element of arrays A, B is an integer within the range [1..2,147,483,647].

  Copyright 2009–2021 by Codility Limited. All Rights Reserved. Unauthorized copying, publication or disclosure prohibited.

How to solve

잘 안풀려서 구글 검색하다 아래 글 참고해서 풀었다 ㅠㅠ

davidespataro.it/solution-to-the-codility-common-prime-divisors-set-problem/

Solution to the Codility Common Prime divisors Set Problem - Davide Spataro

[참고한 글]

 

davidespataro.it/solution-to-the-codility-common-prime-divisors-set-problem/

Solution to the Codility Common Prime divisors Set Problem - Davide Spataro

Solution(c++)

// you can use includes, for example:
#include <bits/stdc++.h>

// you can write to stdout for debugging purposes, e.g.
// cout << "this is a debug message" << endl;

int calc_gcd(int a, int b){
    if(a%b == 0){
        return b;
    }else{
        return calc_gcd(b, a%b);
    }
}

bool check_prime_divisor(int M, int gcd){
    if(M == 1){
        return true;
    }else if(gcd == 1){
        return false;
    }else{
        gcd = calc_gcd(M, gcd);
        M = M/gcd;
        return check_prime_divisor(M, gcd);
    }
}

int solution(vector<int> &A, vector<int> &B) {
    // write your code in C++14 (g++ 6.2.0)
    int len = A.size();
    int count = 0;
    for(int i=0; i<len; i++){
        int num1 = max(A[i], B[i]);
        int num2 = min(A[i], B[i]);
        int gcd = calc_gcd(num1, num2);
        if(check_prime_divisor(num1, gcd) && check_prime_divisor(num2, gcd)){
            count++;
        }
    }
    return count;
}

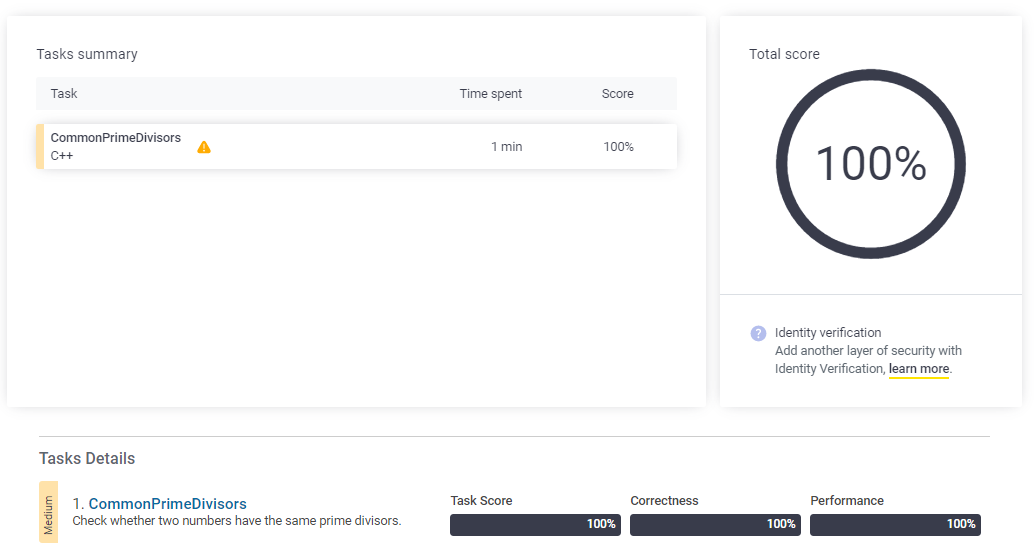
Test Result

app.codility.com/demo/results/trainingUE4RB4-MWP/

Test results - Codility